Show That the Lower Level Sets of a Continuous Function Are Closed
INTRODUTION
In advance analysis, the notion of 'Compact set' is of paramount importance. In ![]() , Heine-Borel theorem provides a very simple characterization of compact sets. The definition and techniques used in connection with compactness of sets in
, Heine-Borel theorem provides a very simple characterization of compact sets. The definition and techniques used in connection with compactness of sets in ![]() are extremely important. In fact, the real line sets the platform to initiate the idea of compactness for the first time and the notion of compactness plays its important role in topological spaces.
are extremely important. In fact, the real line sets the platform to initiate the idea of compactness for the first time and the notion of compactness plays its important role in topological spaces.
The definition of compactness of sets in ![]() uses the notation of open cover of sets in
uses the notation of open cover of sets in ![]() . For this propose we need some definitions and illustrative examples to clear the meaning of cover of a set in
. For this propose we need some definitions and illustrative examples to clear the meaning of cover of a set in ![]() .
.
COVER, OPEN COVER, SUB COVER
Definition (Cover): Let ![]() be subset of
be subset of ![]() and
and ![]() be a collection of sub sets of
be a collection of sub sets of ![]() .
. ![]() is said to cover
is said to cover ![]() or, in other words,
or, in other words, ![]() is said to be a covering of
is said to be a covering of ![]() if
if 
i.e. if ![]() for some
for some ![]() .
.
If ![]() , for each
, for each ![]() , is an open set and
, is an open set and  then
then ![]() is said to be an open cover of
is said to be an open cover of ![]() .
.
For example
Note: If ![]() be a collection of open intervals
be a collection of open intervals ![]() in
in ![]() such that
such that 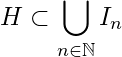 then
then ![]() is also an open cover of
is also an open cover of ![]() .
.
Definition (Sub-Cover): Let ![]() and
and ![]() be a collection of sets in
be a collection of sets in ![]() which covers
which covers ![]() . If
. If ![]() be a sub-collection of such that
be a sub-collection of such that ![]() itself is a cover of
itself is a cover of ![]() then
then ![]() is said to be a sub cover of
is said to be a sub cover of ![]() . If
. If ![]() is a finite sub collection of
is a finite sub collection of ![]() such that
such that ![]() is a cover of
is a cover of ![]() then
then ![]() is said to be a finite sub cover of
is said to be a finite sub cover of ![]() .
.
For example if ![]() then
then 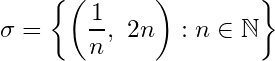 is an open cover of
is an open cover of ![]() .
.
If 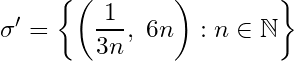 then
then ![]() and
and 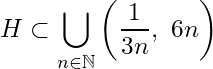 ; this implies
; this implies ![]() is an open sub cover of
is an open sub cover of ![]() .
.
Definition (Countable set): ![]() set
set ![]() in
in ![]() is said to be a countable set if either it is finite or if it is infinite, it is enumerable i.e. there exists a bijective mapping from
is said to be a countable set if either it is finite or if it is infinite, it is enumerable i.e. there exists a bijective mapping from ![]() to
to ![]() .
.
For example
Definition (Countable Sub cover): Let ![]() and
and ![]() be a collection of sets in
be a collection of sets in ![]() such that
such that ![]() covers
covers ![]() . If
. If ![]() be a countable sub-collection of
be a countable sub-collection of ![]() such that
such that ![]() covers
covers ![]() then
then ![]() is said to be a countable sub cover of
is said to be a countable sub cover of ![]() .
.
For example, if ![]() then
then ![]() is an open cover of
is an open cover of ![]() and
and ![]() is a countable sub-collection of
is a countable sub-collection of ![]() , since if
, since if ![]() , the set
, the set ![]() has one-to-one correspondence with
has one-to-one correspondence with ![]() .
. ![]() also covers
also covers ![]() . Hence
. Hence ![]() is a countable sub cover of
is a countable sub cover of ![]() . Note that there are infinitely many countable sub covers of
. Note that there are infinitely many countable sub covers of ![]() , since
, since ![]() is a countable set and
is a countable set and ![]() is the set of open intervals with rational end points and hence
is the set of open intervals with rational end points and hence ![]() itself is a countable family of open sets so that every sub cover of
itself is a countable family of open sets so that every sub cover of ![]() is countable.
is countable.
We now give some examples of open cover of a set in ![]() which has no finite sub cover.
which has no finite sub cover.
Example 1. Let ![]() and
and ![]() where
where ![]() . Show that
. Show that ![]() is an open cover of
is an open cover of ![]() but it has no finite sub cover.
but it has no finite sub cover.
Solution: Let ![]() . Then
. Then ![]() and by the Archimedean property of
and by the Archimedean property of ![]() , there exists a natural number
, there exists a natural number ![]() such that
such that ![]() for some
for some ![]() . Hence
. Hence 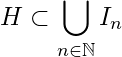 . This shows that
. This shows that ![]() is a collection of open sets in
is a collection of open sets in ![]() which covers
which covers ![]() i.e
i.e ![]() is an open cover of
is an open cover of ![]() .
.
If possible, let ![]() where
where ![]() are natural numbers such that
are natural numbers such that 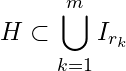 i.e.
i.e. ![]() covers
covers ![]() .
.
Let ![]() then
then ![]() and for
and for ![]()
![]()
Since ![]() but
but ![]() , so we have a contradiction. Hence
, so we have a contradiction. Hence ![]() is not a cover of
is not a cover of ![]() .
.
Thus there exists no finite subcollection of ![]() that will cover
that will cover ![]() .
.
Example 2. Let ![]() and
and ![]() . Show that
. Show that ![]() is an open cover of
is an open cover of ![]() , but it has no finite sub cover.
, but it has no finite sub cover.
Solution: Let ![]() . Then
. Then ![]() . By the Archimedean property of
. By the Archimedean property of ![]() there exists a natural number
there exists a natural number ![]() such that
such that ![]() for some
for some 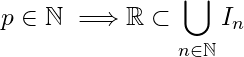 , which shows that
, which shows that ![]() is an open cover of
is an open cover of ![]() (
(![]() is also a countable cover of
is also a countable cover of ![]() ).
).
If possible, let ![]() where
where ![]() are natural numbers such that
are natural numbers such that 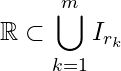 i.e.
i.e. ![]() is a sub cover of
is a sub cover of ![]() .
.
Let ![]() . Then
. Then ![]() and
and ![]() for all
for all ![]() .
.
Thus 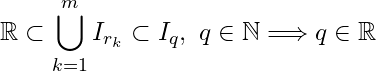 but
but ![]() , a contradiction.
, a contradiction.
Thus it is proved that no finite subcollection of ![]() can cover
can cover ![]() .
.
Example 3. Let ![]() and
and  Let
Let ![]() . Show that
. Show that ![]() is an open cover of
is an open cover of ![]() but no finite subcollection of
but no finite subcollection of ![]() can cover
can cover ![]() .
.
Solution: Let ![]() . Then
. Then ![]() . For
. For 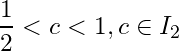 . Let
. Let 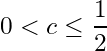 . Then
. Then 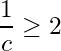 . By the Archimedean property of
. By the Archimedean property of ![]() , there exists a natural number
, there exists a natural number ![]() such that
such that 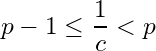 . Since
. Since ![]() ,
, 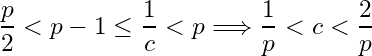 for
for ![]() for some natural number
for some natural number ![]() .
.
Hence 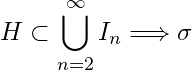 is an open cover of
is an open cover of ![]() .
.
If possible, let ![]() be a finite subcollection of
be a finite subcollection of ![]() , where
, where ![]() are natural numbers
are natural numbers ![]() , such that
, such that 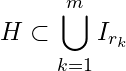 .
.
Let ![]() and
and ![]() then
then 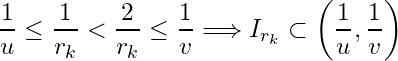 for natural numbers
for natural numbers ![]() .
.
Thus 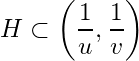 . Since
. Since 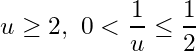 . Hence
. Hence 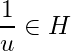 but
but 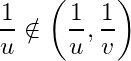 , which is a contradiction. Hence no finite subcollection of
, which is a contradiction. Hence no finite subcollection of ![]() covers
covers ![]() .
.
Example 4. Let ![]() and
and ![]() . Let
. Let ![]() where
where 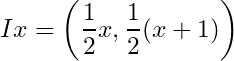 . Show that
. Show that ![]() is an cover of
is an cover of ![]() but it has no finite sub cover.
but it has no finite sub cover.
Solution: Let ![]() . Then
. Then 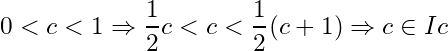 .
.
Hence 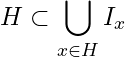 which implies
which implies ![]() is an open cover of
is an open cover of ![]() .
.
If possible, let ![]() where
where ![]() for
for ![]() and
and 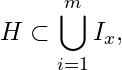 .
.
Let 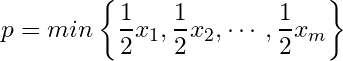
And 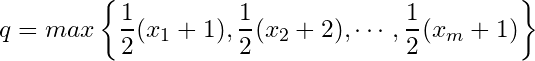 .
.
Then
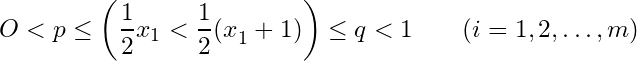
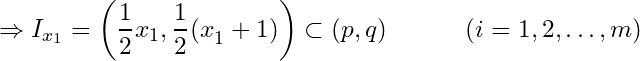
![]() . Since
. Since ![]() but they do not belong to
but they do not belong to ![]() , we have a contradiction. Hence
, we have a contradiction. Hence ![]() has no finite sub-collection that can cover
has no finite sub-collection that can cover ![]() , i.e.
, i.e. ![]() has no finite sub cover.
has no finite sub cover.
Example 5. The collection ![]() of open intervals is an uncountable cover of
of open intervals is an uncountable cover of ![]() but
but ![]() where
where ![]() is the set of integers, is countable sub cover of
is the set of integers, is countable sub cover of ![]() .
.
Solution: Let ![]() . Since
. Since ![]() is both unbounded above and unbounded below, thee always exist two real numbers
is both unbounded above and unbounded below, thee always exist two real numbers ![]() and
and ![]() such that
such that ![]() such that
such that ![]() in
in ![]() such that
such that ![]() . Hence
. Hence ![]() .
.
Thus ![]() . As open interval
. As open interval ![]() is an uncountable subset of
is an uncountable subset of ![]() , so
, so ![]() is an uncountable cover of
is an uncountable cover of ![]() .
.
Thus ![]() . Then by the Archimendeon property of real numbers, there exists an integer
. Then by the Archimendeon property of real numbers, there exists an integer ![]() such that
such that ![]() . This implies
. This implies ![]() for some
for some ![]() . Hence
. Hence ![]() . Thus
. Thus ![]() is a countable sub cover of
is a countable sub cover of ![]() .
.
COMPACT SETS IN 
Definition (Compact set): ![]() set
set ![]() (
(![]() ) is said to be a compact set in
) is said to be a compact set in ![]() if every open cover of
if every open cover of ![]() has a finite sub cover. More explicitly,
has a finite sub cover. More explicitly, ![]() is said to be compact if for any open cover
is said to be compact if for any open cover ![]() of
of ![]() , there is a finite sub collection
, there is a finite sub collection ![]() of
of ![]() such that
such that 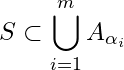 i.e.
i.e. ![]() is a finite sub-cover of
is a finite sub-cover of ![]() .
.
NOTE: To prove that a set ![]() is compact in
is compact in ![]() , we must examine an arbitrary collection of open sets whose union contains
, we must examine an arbitrary collection of open sets whose union contains ![]() , and show that
, and show that ![]() is contained in the union of some finite number of sets in the given collection, i.e. we must have to show that any open cover of
is contained in the union of some finite number of sets in the given collection, i.e. we must have to show that any open cover of ![]() has a finite sub-cover. But to prove that a set
has a finite sub-cover. But to prove that a set ![]() is not compact, it is sufficient to choose one particular open cover
is not compact, it is sufficient to choose one particular open cover ![]() has no finite sub-cover, i.e. union of any finite number of sets in
has no finite sub-cover, i.e. union of any finite number of sets in ![]() fails to contain
fails to contain ![]() .
.
Theorem 1 (Heine-Borel Theorem) :
Statement: –![]() close and bounded subset of
close and bounded subset of ![]() is a compact set in
is a compact set in ![]() , or in other words every open cover of a closed and bounded subset of
, or in other words every open cover of a closed and bounded subset of ![]() has a finite sub cover.
has a finite sub cover.
Proof , Let ![]() be a closed and bounded subset of
be a closed and bounded subset of ![]() .
.
Let ![]() be an open cover of
be an open cover of ![]() . We assume that
. We assume that ![]() has no finite sub-cover. Then
has no finite sub-cover. Then ![]() is not a subject of the union of finite number of open sets in
is not a subject of the union of finite number of open sets in ![]() .
.
Since H is a bounded subject of ![]() , there exist real number
, there exist real number ![]() such that
such that ![]() .
.
Let ![]() . If
. If 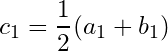 then at least one of the two subsets
then at least one of the two subsets ![]() and
and ![]() are subset of the union of finite number of open sets in
are subset of the union of finite number of open sets in ![]() , for otherwise both
, for otherwise both ![]() and
and ![]() are subsets of the union of finite number of open sets in
are subsets of the union of finite number of open sets in ![]() contains
contains ![]() , contradicting our assumption that
, contradicting our assumption that ![]() has no finite sub-cover.
has no finite sub-cover.
We call ![]() or
or ![]() according as
according as ![]() and it is not a subset of the union of finite number of open sets in
and it is not a subset of the union of finite number of open sets in ![]() or
or ![]() and it is not a subset of the union of finite number of open sets in
and it is not a subset of the union of finite number of open sets in ![]() .
.
Let ![]() and
and 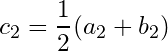 . The at least one of the subsets
. The at least one of the subsets ![]() and
and ![]() is non-empty and it is not a subset of the union of finite number of open sets in
is non-empty and it is not a subset of the union of finite number of open sets in ![]() . If the first subset is non-empty and it is not a subset of the union of finite number of open sets in
. If the first subset is non-empty and it is not a subset of the union of finite number of open sets in ![]() , we call
, we call ![]() , otherwise we call
, otherwise we call ![]() .
.
Let ![]() , and
, and 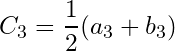 .
.
Continuing this process of bisection of intervals, we have a family of close and bounded intervals ![]() such that
such that
![]() , for all
, for all ![]() ,
,
For all ![]() is non-empty and it is not a subset of the union of finite number of open sets in
is non-empty and it is not a subset of the union of finite number of open sets in ![]() .
.
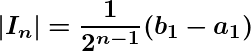 such That
such That ![]() as
as ![]() .
.
Then by Nested Interval Theorem, 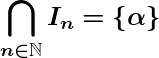 , a singleton set. We shall show that
, a singleton set. We shall show that ![]() .
.
Since ![]() , for any positive
, for any positive ![]() , there exists a natural number
, there exists a natural number ![]() such that
such that ![]() i.e.
i.e. ![]() and
and ![]() . Hence
. Hence ![]() . Since
. Since ![]() and it is not a subset of the union of finite number of open sets in
and it is not a subset of the union of finite number of open sets in ![]() ,
, ![]() contains infinite number of elements of
contains infinite number of elements of ![]() is a limit point of
is a limit point of ![]() . Since
. Since ![]() is closed,
is closed, ![]() .
.
Now ![]() for some
for some ![]() .
. ![]() is an open set, hence there exists a positive
is an open set, hence there exists a positive ![]() and hence
and hence ![]() . Since
. Since ![]() is an open cover of
is an open cover of ![]() ,
, ![]() for some
for some ![]() , which goes against the construction of (
, which goes against the construction of (![]() .
.
Hence our assumption that ![]() is not a subset of the union of finite number of sets in
is not a subset of the union of finite number of sets in ![]() is wrong and it is established that if
is wrong and it is established that if ![]() is closed and bounded, any open cover
is closed and bounded, any open cover ![]() of
of ![]() has a finite sub cover so that
has a finite sub cover so that ![]() is a compact set in
is a compact set in ![]() .
.
Remark: In the Heine-Borel theorem neither of the two conditions (i) ![]() is closed (ii)
is closed (ii) ![]() is bounded can be dropped. The theorem fails if one of the two conditions is withdrawn – this is evident if we go through the example 1.2.3 and the example 1.2.1. In example 1.2.3,
is bounded can be dropped. The theorem fails if one of the two conditions is withdrawn – this is evident if we go through the example 1.2.3 and the example 1.2.1. In example 1.2.3, ![]() is closed but bounded and in example 1.2.1,
is closed but bounded and in example 1.2.1, ![]() is closed but no bounded.
is closed but no bounded.
Thus both the conditions (i) and (ii) are necessary for a set in ![]() to be compact. Next we shall show that these two conditions are also sufficient for a set
to be compact. Next we shall show that these two conditions are also sufficient for a set ![]() to be compact in
to be compact in ![]() .
.
Theorem 2 (Converse of Heine-Borel Theorem):
Statement: –![]() compact subset of
compact subset of ![]() is closed and bounded in
is closed and bounded in ![]() .
.
Proof. Let ![]() be a compact in
be a compact in ![]() . First we shall prove that
. First we shall prove that ![]() is a closed set in
is a closed set in ![]() .
.
Let ![]() and
and ![]() . Then exist two positive numbers
. Then exist two positive numbers ![]() and
and ![]() such that
such that ![]() .
.
Let ![]() .
.
Then ![]() is an open cover of
is an open cover of ![]() is compact,
is compact, ![]() has a finite sub cover i.e. there exist elements
has a finite sub cover i.e. there exist elements ![]() of
of ![]() and positive numbers
and positive numbers ![]() such that
such that 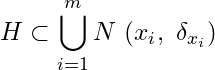 . For each
. For each ![]() there exists positive numbers
there exists positive numbers ![]() such that
such that ![]() .
.
Let ![]() .
.
Then ![]() . Therefore
. Therefore ![]() is an interior point of
is an interior point of ![]() .
.
Since ![]() is arbitrary point of
is arbitrary point of ![]() ,
, ![]() is open. Hence
is open. Hence ![]() is closed.
is closed.
Nest we shall prove that ![]() is bounded.
is bounded.
Let ![]() be a fixed positive number. Then
be a fixed positive number. Then ![]() is an open cover of
is an open cover of ![]() . Since
. Since ![]() is compact,
is compact, ![]() has a finite sub-cover. Then there exist points
has a finite sub-cover. Then there exist points ![]() of
of ![]() such that
such that ![]() is a finite cover of
is a finite cover of ![]() . If
. If ![]() and
and ![]() then
then ![Rendered by QuickLaTeX.com H \subset \bigcup_{i=1}^{m}N(x_i, \delta) \subset [p - \delta, q + \delta] \Rightarrow H](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-99fe79b62f44214eed641b5b3370f6d7_l3.png) is bounded.
is bounded.
Hence it is proved that if ![]() is a compact set in
is a compact set in ![]() , it is closed and bounded in
, it is closed and bounded in ![]() . This completes the proof.
. This completes the proof.
Combining the theorems 1 and 2 we have the following theorem which gives a complete characterization of compact sets in ![]() .
.
Note: – ![]() set in
set in ![]() is compact if and only if is closed and bounded in
is compact if and only if is closed and bounded in ![]() .
.
Definition (Heine-Borel Property): ![]() set
set ![]() (
(![]() ) is said to possess Heine-Borel property if every open cover of
) is said to possess Heine-Borel property if every open cover of ![]() has a finite sub cover.
has a finite sub cover.
![]() set is said to be compacted if it has the Heine-Borel property.
set is said to be compacted if it has the Heine-Borel property.
Example 6. Using the definition of compact set, prove that the set ![]() is not compact although it is a closed set in
is not compact although it is a closed set in ![]() .
.
Solution: In example 1.2.1, it is shown that ![]() , where
, where ![]() , is an open cover of
, is an open cover of ![]() and
and ![]() has no finite sub cover. Hence from definition
has no finite sub cover. Hence from definition ![]() is not compact.
is not compact.
![]() is a closed set in
is a closed set in ![]() , since
, since ![]() is open.
is open.
Note: In the example 1.3.1, ![]() does not satisfy Heine-Borel property, since
does not satisfy Heine-Borel property, since ![]() is not bounded in
is not bounded in ![]() .
.
Example 7. Using definition of compact set show that a finite subset of ![]() is a compact set in
is a compact set in ![]() .
.
Solution: Let ![]() be a finite subset of
be a finite subset of ![]() . Let
. Let ![]() be an open cover of
be an open cover of ![]() . Then each
. Then each ![]() is contained in some open set
is contained in some open set ![]() of
of ![]() for some
for some ![]() . Let
. Let ![]() . Then
. Then 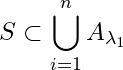 . Thus
. Thus ![]() also covers
also covers ![]() .
.
Hence ![]() is a finite sub cover of
is a finite sub cover of ![]() . Therefore, by definition,
. Therefore, by definition, ![]() is a compact set in
is a compact set in ![]() .
.
Theorem 3.
Statement:– If ![]() be a compact subset of
be a compact subset of ![]() , then every infinite subset of
, then every infinite subset of ![]() has a limit point belonging to
has a limit point belonging to ![]() .
.
Let ![]() be an infinite subset of the compact subset of
be an infinite subset of the compact subset of ![]() of
of ![]() such that
such that ![]() has no limit point belonging to
has no limit point belonging to ![]() .
.
Let ![]() . Then
. Then ![]() is not a limit point of
is not a limit point of ![]() . There exists a positive
. There exists a positive ![]() such that
such that ![]() where
where ![]() , called deleted
, called deleted ![]() .
.
Let ![]() , which is a collection of open sets in
, which is a collection of open sets in ![]() . Since
. Since  so
so ![]() is an open cover of
is an open cover of ![]() .
.
Since ![]() is compact, there exists a finite sub collection
is compact, there exists a finite sub collection ![]() of
of ![]() where
where ![]() and
and ![]() such that
such that ![]() covers
covers ![]() i.e.
i.e. 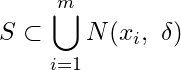
i.e. 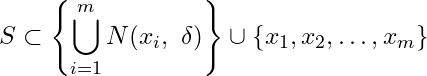
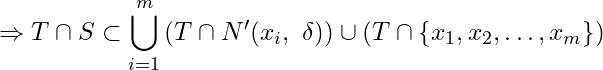
![]()
[Since ![]() and
and ![]() for
for ![]() ]
]
![]()
which shows that ![]() is a finite subset of a compact set
is a finite subset of a compact set ![]() in
in ![]() has a limit point in
has a limit point in ![]() .
.
Theorem 4.
Statement: – If ![]() be such that every infinite subset of
be such that every infinite subset of ![]() has a limit point in
has a limit point in ![]() then
then ![]() is closed and bounded in
is closed and bounded in ![]() .
.
Proof. First we shall prove that ![]() is bounded. If possible, let
is bounded. If possible, let ![]() be unbounded above. Let
be unbounded above. Let ![]() be any point of
be any point of ![]() . Since
. Since ![]() is unbounded above, there exists a point
is unbounded above, there exists a point ![]() in
in ![]() such that
such that ![]() . By similar argument there exists a point
. By similar argument there exists a point ![]() in
in ![]() such that
such that ![]() and so on. Continuing this process indefinitely we ultimately have an infinite subject
and so on. Continuing this process indefinitely we ultimately have an infinite subject ![]() of
of ![]() , which being a discrete set, has no limit point in
, which being a discrete set, has no limit point in ![]() is a bounded above subset of
is a bounded above subset of ![]() . Similarly, If
. Similarly, If ![]() is unbounded below we can construct an infinite subset of
is unbounded below we can construct an infinite subset of ![]() which has no limit point. Hence
which has no limit point. Hence ![]() is also bounded below so that
is also bounded below so that ![]() is a bounded subset of
is a bounded subset of ![]() .
.
Next we shall prove that ![]() is closed in
is closed in ![]() .
.
Since S is an infinite and bounded subset of ![]() , by the Bolzano-Weierstrass theorem on set,
, by the Bolzano-Weierstrass theorem on set, ![]() has a limit point in
has a limit point in ![]() .
.
Let ![]() be a limit point of
be a limit point of ![]() . Then for any
. Then for any ![]() is infinite.
is infinite.
For ![]() is infinite. Let us take a point
is infinite. Let us take a point ![]() .
.
For 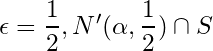 is infinite. Let us take a point
is infinite. Let us take a point ![]() ,
,
such that 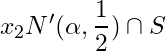 , Continuing this process, we have an infinite subset
, Continuing this process, we have an infinite subset
![]() of
of ![]() such that
such that
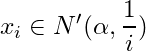 for
for ![]() . We shall show that
. We shall show that ![]() has a unique limit point which is
has a unique limit point which is ![]() .
.
Let ![]() be any positive number. Then by the Archimedean property of
be any positive number. Then by the Archimedean property of ![]() , there exists a natural number
, there exists a natural number ![]() such that
such that 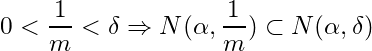 and
and ![]() contains infinite subset
contains infinite subset ![]() of
of ![]() . Thus for every positive
. Thus for every positive ![]() ,
, ![]() is infinite which proves that
is infinite which proves that ![]() is a limit point of
is a limit point of ![]() .
.
To prove uniqueness, let ![]() be a limit point of
be a limit point of ![]() . Let
. Let ![]() . Then the neighborhoods
. Then the neighborhoods ![]() and
and ![]() are disjoint (since either
are disjoint (since either ![]() or
or ![]() ). By the Archimedean property of
). By the Archimedean property of ![]() , there exists a natural number
, there exists a natural number ![]() such that
such that 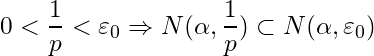 . Since each of
. Since each of ![]() belongs to
belongs to 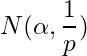 , so
, so ![]() contains all elements of
contains all elements of ![]() expect some finite number of elements and hence
expect some finite number of elements and hence ![]() can contain almost finite number of elements of
can contain almost finite number of elements of ![]() . This implies
. This implies ![]() is not a limit point of
is not a limit point of ![]() . Hence
. Hence ![]() is the only limit point of
is the only limit point of ![]() . By the condition of the theorem
. By the condition of the theorem ![]() . Hence
. Hence ![]() is closed.
is closed.
Thus it is proved that ![]() is closed and bounded in
is closed and bounded in ![]() .
.
Note: – ![]() subset
subset ![]() of a compact subset of
of a compact subset of ![]() is compact if and only if every infinite subset of
is compact if and only if every infinite subset of ![]() has a limit point belonging to
has a limit point belonging to ![]() .
.
Theorem 5.
Statement: – A Subset ![]() of
of ![]() is compact if and only if every sequence in
is compact if and only if every sequence in ![]() has a subsequence that converges to a point in
has a subsequence that converges to a point in ![]() .
.
Proof. Let ![]() be compact. Then
be compact. Then ![]() is closed and bounded.
is closed and bounded.
Let ![]() be a sequence of points in
be a sequence of points in ![]() . Since
. Since ![]() is bounded,
is bounded, ![]() is bounded. By the Bolzano-Weierstrass theorem on sequence, there exists a subsequence
is bounded. By the Bolzano-Weierstrass theorem on sequence, there exists a subsequence ![]() of
of ![]() that converges to a point, say
that converges to a point, say ![]() . Since
. Since ![]() is closed, if
is closed, if ![]() ,
, ![]() and
and ![]() is open. Then there exists a neighborhood
is open. Then there exists a neighborhood ![]() of
of ![]() which contains no point of
which contains no point of ![]() . This implies
. This implies ![]() contains no element of the sequence
contains no element of the sequence ![]() which contradicts that
which contradicts that ![]() . Thus
. Thus ![]() . Hence every sequence in
. Hence every sequence in ![]() has a subsequence converging to a point of
has a subsequence converging to a point of ![]() .
.
Suppose ![]() is not closed. Then
is not closed. Then ![]() has a limit point, say
has a limit point, say ![]() which is not in
which is not in ![]() . Since
. Since ![]() is a limit point of
is a limit point of ![]() , there is a sequence
, there is a sequence ![]() in
in ![]() , where
, where ![]() for all
for all ![]() , such that
, such that ![]() . Then every subsequence of
. Then every subsequence of ![]() converges to
converges to ![]() . Since
. Since ![]() , there is no subsequence of
, there is no subsequence of ![]() that converges to a point of
that converges to a point of ![]() .
.
Suppose ![]() is not bounded. Then there exists a sequence
is not bounded. Then there exists a sequence ![]() in
in ![]() such that
such that ![]() for all
for all ![]() . Then every subsequence of unbounded sequence
. Then every subsequence of unbounded sequence ![]() is unbounded and hence no subsequence of
is unbounded and hence no subsequence of ![]() converges to a point in
converges to a point in ![]() .
.
Hence, by contrapositive argument, it is proved that if every sequence in ![]() has a subsequence that converges to a point of
has a subsequence that converges to a point of ![]() the
the ![]() is closed and bounded and hence by Heine-Borel theorem
is closed and bounded and hence by Heine-Borel theorem ![]() is compact.
is compact.
Note: Following theorem 5., an alternative definition of compact set can be given in the from:
"A set ![]() in
in ![]() is called a compact set in
is called a compact set in ![]() if every sequence in
if every sequence in ![]() has a subsequence that converges to a point of
has a subsequence that converges to a point of ![]() ."
."
Theorem 5 and the Heine-Borel theorem together prove the equivalence of the two definitions.
Example 8. If ![]() is a closed subset of a compact set
is a closed subset of a compact set ![]() in
in ![]() then using definition of compact set, prove that
then using definition of compact set, prove that ![]() is compact.
is compact.
Solution: ![]() is open, since
is open, since ![]() is closed.
is closed.
Let ![]() be an open cover of
be an open cover of ![]() . Suppose
. Suppose ![]() is not an open cover of
is not an open cover of ![]() . Let
. Let ![]() . Then
. Then 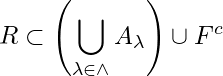 i.e.,
i.e., ![]() is an open cover of
is an open cover of ![]() . Since
. Since ![]() ,
, ![]() is also an open cover of
is also an open cover of ![]() .
. ![]() being compact,
being compact, ![]() has a finite sub collection
has a finite sub collection ![]() such that
such that 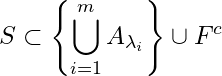 , where
, where ![]() .
. ![]() must contain
must contain ![]() , otherwise
, otherwise 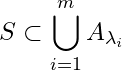 which implies
which implies ![]() is an open cover of
is an open cover of ![]() , which is contrary to our assumption.
, which is contrary to our assumption.
Since ![]() we have
we have 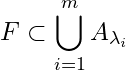 .
.
Which shows that,
![]() is a finite sub collection of
is a finite sub collection of ![]() and
and ![]() covers
covers ![]() , which implies
, which implies ![]() is a finite sub cover of
is a finite sub cover of ![]() . Therefore, by definition,
. Therefore, by definition, ![]() is compact.
is compact.
Example 9. Every compact set in ![]() has greatest as well as least element.
has greatest as well as least element.
Solution: Let ![]() be any compact set in
be any compact set in ![]() . If possible, let
. If possible, let ![]() have no greatest element. Then for each element
have no greatest element. Then for each element ![]() . let
. let ![]() . Then
. Then ![]() is an open set. Let
is an open set. Let ![]() , a family of open sets in
, a family of open sets in ![]() . Let
. Let ![]() . Since
. Since ![]() has no greatest element, there exists an element
has no greatest element, there exists an element ![]() in
in ![]() such that
such that ![]() . Thus
. Thus ![]() . Hence
. Hence ![]() is an open cover of
is an open cover of ![]() .
. ![]() being compact,
being compact, ![]() has a finite sub-cover, say
has a finite sub-cover, say ![]() .
.
Let ![]() Then
Then ![]() for
for ![]() and
and 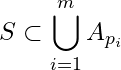 . Let
. Let ![]() .
.
Then ![]() and
and ![]() . This leads to a contradiction, since
. This leads to a contradiction, since ![]() . Hence our assumption is not tenable and
. Hence our assumption is not tenable and ![]() has greatest element.
has greatest element.
To prove the next part, let, if possible, ![]() has no least element. Then for each element
has no least element. Then for each element ![]() , let
, let ![]() is an open set. Let
is an open set. Let ![]() , a family of open sets in
, a family of open sets in ![]() . Let
. Let ![]() . Since
. Since ![]() has no least element there exists an element
has no least element there exists an element ![]() in
in ![]() such that
such that ![]() . Then
. Then ![]() and
and ![]() . Thus
. Thus ![]() is an open cover of
is an open cover of ![]() . Since
. Since ![]() is compact,
is compact, ![]() has a finite sub collection
has a finite sub collection ![]() that covers
that covers ![]() .
.
Let ![]() where
where ![]() and
and 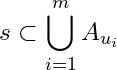 . If
. If ![]() then
then ![]() .
.
Now ![]() but
but ![]() which contradicts our assumption. Hence
which contradicts our assumption. Hence ![]() has least element.
has least element.
Example 10. If ![]() and
and ![]() are component sets in
are component sets in ![]() , show that
, show that ![]() is also compact. Give an example to show that union of an infinite number of compact sets in
is also compact. Give an example to show that union of an infinite number of compact sets in ![]() is not necessarily a compact set in
is not necessarily a compact set in ![]() .
.
Solution: Let ![]() be a family of open sets in
be a family of open sets in ![]() such that
such that 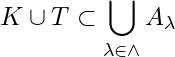 i.e.
i.e. ![]() is an open cover of
is an open cover of ![]() .
.
Since 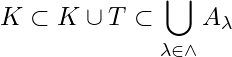 and
and 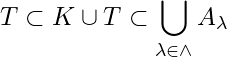 ,
,
![]() is an open cover of both
is an open cover of both ![]() and
and ![]() . Since
. Since ![]() and
and ![]() are both compact sets in
are both compact sets in ![]() , then there exist two finite sub collections
, then there exist two finite sub collections
![]() and
and ![]() of
of ![]() such that
such that
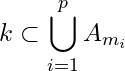 and
and 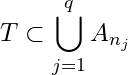 where
where ![]() and
and ![]() .
.
Let ![]() . Then
. Then ![]() is a finite sub collection of
is a finite sub collection of ![]() such that
such that
![]() or
or ![]()
![]() for some
for some ![]()
Or ![]() for some
for some ![]()
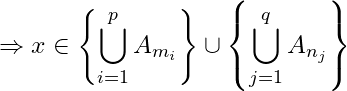
Hence 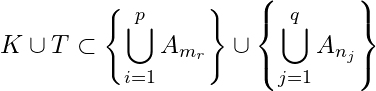
![]() cover
cover ![]() . Hence, from definition,
. Hence, from definition, ![]() is compact.
is compact.
Second Part.
Let ![]() . Then for each
. Then for each ![]() ,
, ![]() is closed and bounded set in
is closed and bounded set in ![]() and by Heine-Borel Theorem,
and by Heine-Borel Theorem, ![]() is compact for every
is compact for every ![]() . Thus
. Thus ![]() is an infinite collection of compact sets in
is an infinite collection of compact sets in ![]() .
.
But 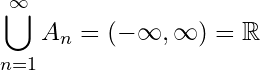 , which is not a compact set (see example 1.2.2). Hence union of infinite number of compact sets in
, which is not a compact set (see example 1.2.2). Hence union of infinite number of compact sets in ![]() is not necessarily compact.
is not necessarily compact.
Example 11. Let ![]() be a closed subset of
be a closed subset of ![]() and
and ![]() be a component subset of
be a component subset of ![]() . Prove that
. Prove that ![]() is component.
is component.
Solution: Since ![]() is compact, by converse of Heine-Borel theorem
is compact, by converse of Heine-Borel theorem ![]() is closed.
is closed. ![]() being closed,
being closed, ![]() is a closed subset of compact set
is a closed subset of compact set ![]() . Then following exactly similar arguments given in example 1.3.3 (replacing
. Then following exactly similar arguments given in example 1.3.3 (replacing  \mathbb{R}
\mathbb{R} \sigma = \{C\}
\sigma = \{C\}![]() \mathbb{R}
\mathbb{R}![]() S =\ \bigcap_{C\in\sigma} C
S =\ \bigcap_{C\in\sigma} C![]() C
C![]() \sigma
\sigma![]() S
S![]() R
R![]() \mathbb{R}-S
\mathbb{R}-S![]() g' = \{G : \alpha \in \Lambda\}
g' = \{G : \alpha \in \Lambda\}![]() \mathbb{R}
\mathbb{R}![]() S
S![]() S \subset \ \bigcap_{\alpha\in\land} G_\alpha
S \subset \ \bigcap_{\alpha\in\land} G_\alpha![]() g
g![]() C
C![]() C \in \sigma
C \in \sigma![]() g'
g'![]() \{G : \alpha \in \Lambda\}
\{G : \alpha \in \Lambda\}![]() \mathbb{R} – S
\mathbb{R} – S![]() \mathbb{R} \subset \left\lbrace\bigcup_{\alpha\in\land} G_\alpha\right\rbrace \cup \left(\mathbb{R} – S\right)
\mathbb{R} \subset \left\lbrace\bigcup_{\alpha\in\land} G_\alpha\right\rbrace \cup \left(\mathbb{R} – S\right)![]() C \subset \mathbb{R}
C \subset \mathbb{R}![]() C \subset \left\lbrace \bigcup_{\alpha\in\land} G_\alpha\right\rbrace \cup \left(\mathbb{R} – S\right)
C \subset \left\lbrace \bigcup_{\alpha\in\land} G_\alpha\right\rbrace \cup \left(\mathbb{R} – S\right)![]() C \in \sigma
C \in \sigma![]() g'
g'![]() C
C![]() C \in \sigma
C \in \sigma![]() C
C![]() C \in \sigma
C \in \sigma![]() g"
g"![]() g'
g'![]() g"
g"![]() C
C![]() C \in \sigma
C \in \sigma![]() f" = \{G_{\alpha_1},\ G_{\alpha_2}, \ldots,\ G_{\alpha_m},\ \mathbb{R}\ – S\}
f" = \{G_{\alpha_1},\ G_{\alpha_2}, \ldots,\ G_{\alpha_m},\ \mathbb{R}\ – S\}![]() g"
g"![]() \mathbb{R} – S
\mathbb{R} – S![]() C \subset \bigcup_{i=1}^{m}G_{\alpha_i}
C \subset \bigcup_{i=1}^{m}G_{\alpha_i}![]() g
g![]() C
C![]() C \in \sigma
C \in \sigma![]() C \subset \left\lbrace\bigcup_{i=1}^{m}G_{\alpha_i}\right\rbrace \cup (\mathbb{R} – S)
C \subset \left\lbrace\bigcup_{i=1}^{m}G_{\alpha_i}\right\rbrace \cup (\mathbb{R} – S)![]() C \in \sigma
C \in \sigma![]() S \subset C
S \subset C![]() S \subset \bigcup_{i=1}^{m}G_{\alpha_i}
S \subset \bigcup_{i=1}^{m}G_{\alpha_i}![]() g"' = \{G_{\alpha_1},\ G_{\alpha_2}, \ldots,\ G_{\alpha_m}\}
g"' = \{G_{\alpha_1},\ G_{\alpha_2}, \ldots,\ G_{\alpha_m}\}![]() g"'
g"'![]() g
g![]() S
S![]() g
g![]() S
S (0, 1]
(0, 1]![]() \mathbb{R}
\mathbb{R}![]() I_n = \left(\frac{1}{n+1},\ \frac{n+1}{n}\right), n \in \mathbb{N}
I_n = \left(\frac{1}{n+1},\ \frac{n+1}{n}\right), n \in \mathbb{N}![]() \sigma = \{I_n : n \in \mathbb{N}\}
\sigma = \{I_n : n \in \mathbb{N}\}![]() \sigma
\sigma![]() \mathbb{R}
\mathbb{R}![]() x \in (0, 1]
x \in (0, 1]![]() x = 1
x = 1![]() x \in I_n
x \in I_n![]() n \in \mathbb{N}
n \in \mathbb{N}![]() 0< x < 1
0< x < 1![]() \mathbb{R}
\mathbb{R}![]() m
m![]() m \le\ \frac{1}{x} < m + 1
m \le\ \frac{1}{x} < m + 1
\Rightarrow \frac{1}{m+1} < x \le\ \frac{1}{m} <\ \frac{m+1}{m} \Rightarrow x \in I_m![]() m \in \mathbb{N}
m \in \mathbb{N}![]() (0, 1] \subset \bigcup_{n\in\mathbb{N}} I_n
(0, 1] \subset \bigcup_{n\in\mathbb{N}} I_n![]() \sigma
\sigma![]() (0, 1]
(0, 1]![]() \sigma' = \{I_{r_1},\ I_{r_2}, \ldots,\ I_{r_m}\}
\sigma' = \{I_{r_1},\ I_{r_2}, \ldots,\ I_{r_m}\}![]() \sigma
\sigma![]() r_1, r_2, \ldots, r_m
r_1, r_2, \ldots, r_m![]() (0, 1] \subset \bigcup_{k=1}^{m}I_{r_k}
(0, 1] \subset \bigcup_{k=1}^{m}I_{r_k}![]() u = \max \{r_1 + 1, r_2 + 1,\ldots, r_m + 1\} \Rightarrow u \geq r_k + 1
u = \max \{r_1 + 1, r_2 + 1,\ldots, r_m + 1\} \Rightarrow u \geq r_k + 1![]() k = 1, 2, \ldots, m
k = 1, 2, \ldots, m![]() v = \min \{\frac{r_1}{r_1+ 1},\ \frac{r_2}{r_2+ 1}, \ldots,\ \frac{r_m}{r_m+\ 1}\} \Rightarrow v \leq \frac{r_k}{r_k+ 1}
v = \min \{\frac{r_1}{r_1+ 1},\ \frac{r_2}{r_2+ 1}, \ldots,\ \frac{r_m}{r_m+\ 1}\} \Rightarrow v \leq \frac{r_k}{r_k+ 1}![]() k = 1, 2, \ldots, m
k = 1, 2, \ldots, m![]() 0 < \frac{1}{u} \leq \frac{1}{r_k+ 1} < \frac{r_k+ 1}{r_k} \leq \frac{1}{v},\ x = 1, 2,\ldots, m\Rightarrow I_{r_k} \subset \left(\frac{1}{u},\ \frac{1}{v}\right)
0 < \frac{1}{u} \leq \frac{1}{r_k+ 1} < \frac{r_k+ 1}{r_k} \leq \frac{1}{v},\ x = 1, 2,\ldots, m\Rightarrow I_{r_k} \subset \left(\frac{1}{u},\ \frac{1}{v}\right)![]() k = 1, 2,\ldots, m\Rightarrow (0, 1] \subset \left(\frac{1}{u},\ \frac{1}{v}\right)
k = 1, 2,\ldots, m\Rightarrow (0, 1] \subset \left(\frac{1}{u},\ \frac{1}{v}\right)![]() 0 < \frac{1}{u} < 1
0 < \frac{1}{u} < 1![]() \frac{1}{u} \in (0, 1]
\frac{1}{u} \in (0, 1]![]() \frac{1}{u} \left(\frac{1}{u},\ \frac{1}{v}\right)
\frac{1}{u} \left(\frac{1}{u},\ \frac{1}{v}\right)![]() \sigma
\sigma![]() (0, 1]
(0, 1]![]() (0, 1]
(0, 1]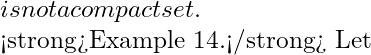 a < x < b
a < x < b![]() \Gamma = \{(x – \varepsilon, x + \varepsilon), \varepsilon > 0\}
\Gamma = \{(x – \varepsilon, x + \varepsilon), \varepsilon > 0\}![]() \Gamma
\Gamma![]() [a, b]
[a, b]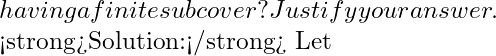 I_x = (x – \varepsilon, x + \varepsilon),\ \varepsilon > 0
I_x = (x – \varepsilon, x + \varepsilon),\ \varepsilon > 0![]() a < x < b
a < x < b![]() \Gamma = \{I_x : a < x < b\}
\Gamma = \{I_x : a < x < b\}![]() x
x![]() (a, b)
(a, b)![]() I_x
I_x![]() \mathbb{R}
\mathbb{R}![]() x_1, x_2 \in (a, b)
x_1, x_2 \in (a, b)![]() a < x_1 < a + \varepsilon
a < x_1 < a + \varepsilon![]() b – \varepsilon < x_2 < b
b – \varepsilon < x_2 < b![]() x_1 – \varepsilon < a,\ x_1 + \varepsilon > a
x_1 – \varepsilon < a,\ x_1 + \varepsilon > a![]() b < x_2 + \varepsilon, x_2 – \varepsilon < b
b < x_2 + \varepsilon, x_2 – \varepsilon < b![]() a \in I_{x_1}
a \in I_{x_1}![]() b \in I_{x_2}
b \in I_{x_2}![]() [a, b] \subset \bigcap_{a<x<b} I_x \Rightarrow \Gamma
[a, b] \subset \bigcap_{a<x<b} I_x \Rightarrow \Gamma![]() [a, b]
[a, b]![]() [a, b]
[a, b]![]() \Gamma
\Gamma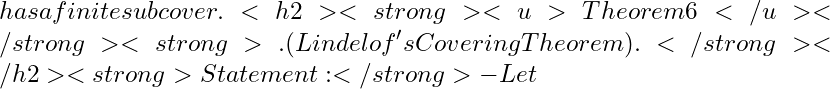 S \subset\mathbb{R}
S \subset\mathbb{R}![]() S
S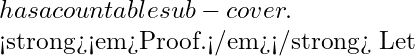 C = \{A : \alpha \in \Lambda\}
C = \{A : \alpha \in \Lambda\}![]() A_\alpha
A_\alpha![]() \mathbb{R}
\mathbb{R}![]() \Lambda
\Lambda![]() S
S![]() S \subset \bigcup_{\alpha\in\land} A_\alpha
S \subset \bigcup_{\alpha\in\land} A_\alpha![]() x \in S
x \in S![]() \alpha(x) \in \Lambda
\alpha(x) \in \Lambda![]() x \in A_{\alpha(x)}
x \in A_{\alpha(x)}![]() A_{\alpha(x)}
A_{\alpha(x)}![]() x
x![]() I(x)
I(x)![]() x
x![]() x \in I(x) \subset A_{\alpha(x)}
x \in I(x) \subset A_{\alpha(x)}![]() I(x)
I(x)![]() J(x) \subset I(x)
J(x) \subset I(x)![]() x \in J(x)
x \in J(x)![]() j(x)
j(x)![]() S \subset \bigcup_{x\in S} I\left(x\right)
S \subset \bigcup_{x\in S} I\left(x\right)![]() \{J(x) : x \in S\}
\{J(x) : x \in S\}![]() S
S![]() \{J(x) : x \in S\}
\{J(x) : x \in S\}![]() C' = \{j_1, j_2, j_3, \ldots\}
C' = \{j_1, j_2, j_3, \ldots\}![]() S
S![]() J_n \in C'
J_n \in C'![]() x_n \in S
x_n \in S![]() x_n \in J_n \subset I(x_n) \subset A_{\alpha_n}
x_n \in J_n \subset I(x_n) \subset A_{\alpha_n}![]() J_n \in C'
J_n \in C'![]() A_{\alpha_n} \in C
A_{\alpha_n} \in C![]() C" = \{A_{\alpha_1},\ A_{\alpha_2}, \ldots,\ A_{\alpha_n}, \ldots\}
C" = \{A_{\alpha_1},\ A_{\alpha_2}, \ldots,\ A_{\alpha_n}, \ldots\}![]() C"
C"![]() C
C![]() S
S \bm{\{0\} \cup \left\{ }\frac{\bm{1}}{\bm{n}}\bm{:n\in\ \mathbb{N}\right\rbrace}
\bm{\{0\} \cup \left\{ }\frac{\bm{1}}{\bm{n}}\bm{:n\in\ \mathbb{N}\right\rbrace} S =\left\lbrace 0,\ 1,\ \frac{1}{2},\ \frac{1}{3}, \ldots\right\rbrace
S =\left\lbrace 0,\ 1,\ \frac{1}{2},\ \frac{1}{3}, \ldots\right\rbrace![]() T
T![]() S
S![]() T = \left\lbrace 0,\ \frac{1}{m}\ :m\ \in\ N_1\right\rbrace
T = \left\lbrace 0,\ \frac{1}{m}\ :m\ \in\ N_1\right\rbrace![]() T = \left\lbrace\frac{1}{m}\ :m\ \in\ N_1\right\rbrace
T = \left\lbrace\frac{1}{m}\ :m\ \in\ N_1\right\rbrace![]() N_1
N_1![]() \mathbb{N}
\mathbb{N}![]() 0
0![]() T
T![]() 0 \in S
0 \in S![]() S
S![]() S
S![]() S
S![]() S
S \mathbb{R}
\mathbb{R}![]() \mathbb{R}
\mathbb{R}![]() A = \left\lbrace\frac{1}{m}+\frac{1}{n}\ :m\ \in\ \mathbb{N},\ n\ \in\mathbb{N}\right\rbrace
A = \left\lbrace\frac{1}{m}+\frac{1}{n}\ :m\ \in\ \mathbb{N},\ n\ \in\mathbb{N}\right\rbrace![]() B = \left\lbrace 0,\ \frac{1}{m}\ :m\ \in\ \mathbb{N}\right\rbrace
B = \left\lbrace 0,\ \frac{1}{m}\ :m\ \in\ \mathbb{N}\right\rbrace![]() C = \{0\}
C = \{0\}![]() S = A \cup B \cup C
S = A \cup B \cup C![]() \mathbb{R}
\mathbb{R}![]() S \subset [0, 2]
S \subset [0, 2]![]() A,\ B,\ C
A,\ B,\ C![]() A' =\left\lbrace 0,\ \frac{1}{m}\ :m\ \in\ \mathbb{N}\right\rbrace
A' =\left\lbrace 0,\ \frac{1}{m}\ :m\ \in\ \mathbb{N}\right\rbrace![]() B' = \{0\}
B' = \{0\}![]() C' = \emptyset
C' = \emptyset![]() S' = A' \cup B' \cup C' = \{0\} \cup \left\lbrace\frac{1}{m}\ :m\ \in\ \mathbb{N}\right\rbrace = B \cup C \subset S
S' = A' \cup B' \cup C' = \{0\} \cup \left\lbrace\frac{1}{m}\ :m\ \in\ \mathbb{N}\right\rbrace = B \cup C \subset S![]() S
S![]() S
S![]() \mathbb{R}
\mathbb{R}![]() S
S![]() \mathbb{R}
\mathbb{R}![]() f : \mathbb{N} \to B
f : \mathbb{N} \to B![]() f(m) = \frac{1}{m},\ m \in\ \mathbb{N}
f(m) = \frac{1}{m},\ m \in\ \mathbb{N}![]() B
B![]() S'
S'![]() S'
S'![]() \mathbb{R}
\mathbb{R} \{F_n\}_n
\{F_n\}_n![]() \mathbb{R}
\mathbb{R}![]() \bigcap_{n\in\mathbb{N}} F_n
\bigcap_{n\in\mathbb{N}} F_n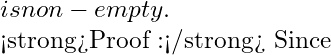 \{F_n\}_n
\{F_n\}_n![]() F_n \supset F_{n+1}
F_n \supset F_{n+1}![]() n \in \mathbb{N}
n \in \mathbb{N}![]() F_n
F_n![]() n \in \mathbb{N}
n \in \mathbb{N}![]() F_n \neq \emptyset
F_n \neq \emptyset![]() n \in \mathbb{N}
n \in \mathbb{N}![]() x_n \in F_n
x_n \in F_n![]() \{x_n\}_n
\{x_n\}_n![]() x_n \in F_n \subset F_m
x_n \in F_n \subset F_m![]() m \leq n
m \leq n![]() X
X![]() \{x_n\}_n
\{x_n\}_n![]() X
X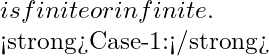 X
X![]() \alpha \in X
\alpha \in X![]() x_n = \alpha
x_n = \alpha![]() n
n![]() \mathbb{N}
\mathbb{N}![]() p \in \mathbb{N}
p \in \mathbb{N}![]() k \geq p
k \geq p![]() x_k = \alpha
x_k = \alpha![]() \alpha = x_k \in F_k \subset F_p
\alpha = x_k \in F_k \subset F_p![]() p \in \mathbb{N}
p \in \mathbb{N}![]() \alpha \in \bigcap_{n\in\mathbb{N}} F_n \Rightarrow \bigcap_{n\in\mathbb{N}} F_n \neq \emptyset
\alpha \in \bigcap_{n\in\mathbb{N}} F_n \Rightarrow \bigcap_{n\in\mathbb{N}} F_n \neq \emptyset![]() X
X![]() F_n
F_n![]() F_1 \supset X
F_1 \supset X![]() X
X![]() X
X![]() \beta
\beta![]() m
m![]() \beta
\beta![]() X
X![]() \beta
\beta![]() N(\beta)
N(\beta)![]() X
X![]() N(\beta)
N(\beta)![]() x_n
x_n![]() x_n \in F_m
x_n \in F_m![]() n \geq m
n \geq m![]() N(\beta) \cap F_m
N(\beta) \cap F_m![]() \beta
\beta![]() F_m
F_m![]() F_m
F_m![]() \beta \in F_m
\beta \in F_m![]() m \in \mathbb{N}
m \in \mathbb{N}![]() \beta \in \bigcap_{n\in\mathbb{N}} F_n \Rightarrow \bigcap_{n\in\mathbb{N}}{F^\prime}_n \neq \emptyset
\beta \in \bigcap_{n\in\mathbb{N}} F_n \Rightarrow \bigcap_{n\in\mathbb{N}}{F^\prime}_n \neq \emptyset![]() \bigcap_{n\in\mathbb{N}}{F^\prime}_n
\bigcap_{n\in\mathbb{N}}{F^\prime}_n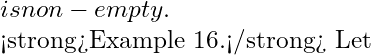 E = \{r \in \mathbb{Q} : \sqrt{2} < r < \sqrt{3} \}
E = \{r \in \mathbb{Q} : \sqrt{2} < r < \sqrt{3} \}![]() E
E![]() \mathbb{Q}
\mathbb{Q}![]() E
E![]() \mathbb{Q}
\mathbb{Q}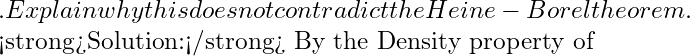 \mathbb{R}
\mathbb{R}![]() x_1
x_1![]() y_1
y_1![]() E
E![]() \subset \mathbb{Q}
\subset \mathbb{Q}![]() \sqrt{2} < x_1 < y_1 < \sqrt{3}
\sqrt{2} < x_1 < y_1 < \sqrt{3}![]() x_2
x_2![]() y_2
y_2![]() E
E![]() \sqrt{2} < x_2 < x_1 < y_1 < x_2 < \sqrt3
\sqrt{2} < x_2 < x_1 < y_1 < x_2 < \sqrt3![]() E
E![]() \{x_n\}_n
\{x_n\}_n![]() \{y_n\}_n
\{y_n\}_n![]() \{x_n\}_n
\{x_n\}_n![]() \sqrt{2}
\sqrt{2}![]() \{y_n\}_n
\{y_n\}_n![]() \sqrt3
\sqrt3![]() \sigma = \{I_n : n \in \mathbb{N}\}
\sigma = \{I_n : n \in \mathbb{N}\}![]() I_n = (x_n,\ y_n)
I_n = (x_n,\ y_n)![]() \sqrt2 < x_n < y_n < \sqrt3
\sqrt2 < x_n < y_n < \sqrt3![]() n \in \mathbb{N}
n \in \mathbb{N}![]() x_n \in \mathbb{Q}
x_n \in \mathbb{Q}![]() y_n \in \mathbb{Q}
y_n \in \mathbb{Q}![]() m \in \mathbb{N}
m \in \mathbb{N}![]() x \in E
x \in E![]() x \in I_m
x \in I_m![]() m \in \mathbb{N}
m \in \mathbb{N}![]() E \subset\bigcup_{n\in\mathbb{N}} I_n
E \subset\bigcup_{n\in\mathbb{N}} I_n![]() \sigma
\sigma![]() E
E![]() \sigma' = \{I_{r_1},\ I_{r_2}, \ldots,\ I_{r_m}\}
\sigma' = \{I_{r_1},\ I_{r_2}, \ldots,\ I_{r_m}\}![]() \sigma
\sigma![]() \sigma'
\sigma'![]() E
E![]() r_1, r_2,\ldots, r_m
r_1, r_2,\ldots, r_m![]() E \subset \bigcup_{i=1}^{m}I_{r_i}
E \subset \bigcup_{i=1}^{m}I_{r_i}![]() p = \max \{r_1, r_2,\ldots, r_m\}
p = \max \{r_1, r_2,\ldots, r_m\}![]() p \in \mathbb{N}
p \in \mathbb{N}![]() I_{r_i} \subset I_p
I_{r_i} \subset I_p![]() I = 1, 2, \ldots, m
I = 1, 2, \ldots, m![]() E \subset I_p = (x_p,\ y_p)
E \subset I_p = (x_p,\ y_p)![]() \sqrt2 < y_p < \sqrt3 \Rightarrow y_p \in E
\sqrt2 < y_p < \sqrt3 \Rightarrow y_p \in E![]() y_p \notin I_p
y_p \notin I_p![]() \sigma
\sigma![]() E
E![]() \mathbb{Q}
\mathbb{Q}![]() E
E![]() \mathbb{Q}
\mathbb{Q}![]() x \in E \Rightarrow 1 < \sqrt2 < x < \sqrt3 < 2
x \in E \Rightarrow 1 < \sqrt2 < x < \sqrt3 < 2![]() 1
1![]() 2
2![]() E
E![]() \mathbb{Q}
\mathbb{Q} E
E![]() \mathbb{Q}
\mathbb{Q}![]() p < \sqrt2
p < \sqrt2![]() \mathbb{R}
\mathbb{R}![]() r
r![]() p < r < \sqrt2
p < r < \sqrt2![]() \delta
\delta![]() p
p![]() \delta = r – p > 0
\delta = r – p > 0![]() (p – \delta, p + \delta)
(p – \delta, p + \delta)![]() E
E![]() p + \delta = r < \sqrt2
p + \delta = r < \sqrt2![]() (p – \delta, p + \delta) \cap E = \emptyset \Rightarrow p
(p – \delta, p + \delta) \cap E = \emptyset \Rightarrow p![]() E
E![]() q > \sqrt3
q > \sqrt3![]() \mathbb{R}
\mathbb{R}![]() \sqrt3 <s < q
\sqrt3 <s < q![]() \delta' = q – s > 0
\delta' = q – s > 0![]() \delta'
\delta'![]() q
q![]() (p – \delta', p + \delta')
(p – \delta', p + \delta')![]() E
E![]() q – \delta' = s > \sqrt3
q – \delta' = s > \sqrt3![]() (p – \delta', p + \delta') \cap E = \emptyset \Rightarrow q
(p – \delta', p + \delta') \cap E = \emptyset \Rightarrow q![]() E
E![]() E
E![]() E
E![]() E
E![]() E
E![]() E
E![]() \mathbb{Q}
\mathbb{Q} \mathbb{R}
\mathbb{R}![]() \mathbb{Q}
\mathbb{Q} \bm{\mathbb{R}}
\bm{\mathbb{R}} E
E![]() \mathbb{R}
\mathbb{R}![]() \sigma
\sigma![]() \mathbb{R}
\mathbb{R}![]() E
E![]() \sigma
\sigma![]() \sigma'
\sigma'![]() \sigma'
\sigma'![]() \sigma'
\sigma'![]() \sigma' = \{I_n : n \in \mathbb{N}\}
\sigma' = \{I_n : n \in \mathbb{N}\}![]() \sigma'
\sigma'![]() E
E![]() E \subset\bigcup_{n\in\mathbb{N}} I_n
E \subset\bigcup_{n\in\mathbb{N}} I_n![]() A_n = E \cap \left(\bigcup_{k=1}^{n}I_k\right)^c = E – \bigcup_{k=1}^{n}I_k (n = 1, 2, 3,\ldots.)
A_n = E \cap \left(\bigcup_{k=1}^{n}I_k\right)^c = E – \bigcup_{k=1}^{n}I_k (n = 1, 2, 3,\ldots.)![]() A_n \supset A_{n+1}
A_n \supset A_{n+1}![]() n \in \mathbb{N}
n \in \mathbb{N}![]() \bigcup_{k=1}^{n}I_k
\bigcup_{k=1}^{n}I_k![]() E
E![]() \mathbb{R}
\mathbb{R}![]() n \in \mathbb{N}
n \in \mathbb{N}![]() A_n
A_n![]() \mathbb{R}
\mathbb{R}![]() \{A_n\}
\{A_n\} A_n \neq \emptyset
A_n \neq \emptyset![]() n \in \mathbb{N}
n \in \mathbb{N}![]() \bigcap_{n\in\mathbb{N}} A_n \neq \emptyset \Rightarrow
\bigcap_{n\in\mathbb{N}} A_n \neq \emptyset \Rightarrow![]() c \in \bigcap_{n\in\mathbb{N}} A_n \Rightarrow c \in E
c \in \bigcap_{n\in\mathbb{N}} A_n \Rightarrow c \in E![]() c \notin I_n
c \notin I_n![]() n \in \mathbb{N}
n \in \mathbb{N}![]() c \notin \bigcup_{n\in\mathbb{N}} I_n
c \notin \bigcup_{n\in\mathbb{N}} I_n![]() \sigma'
\sigma'![]() E
E![]() A_m = \emptyset \Rightarrow E \subset \bigcup_{k=1}^{m}I_k
A_m = \emptyset \Rightarrow E \subset \bigcup_{k=1}^{m}I_k![]() \sigma" = \{I_1, I_2, \ldots, I_m\}
\sigma" = \{I_1, I_2, \ldots, I_m\}![]() \sigma'
\sigma'![]() \sigma
\sigma![]() E
E![]() E
E![]() E
E f : S \to \mathbb{R}
f : S \to \mathbb{R}![]() S \subset \mathbb{R}
S \subset \mathbb{R}![]() S
S![]() c \in S
c \in S![]() f
f![]() c
c![]() \varepsilon> 0
\varepsilon> 0![]() (\varepsilon, 0) > 0
(\varepsilon, 0) > 0![]() f(c)\ – \varepsilon < f(x) < f(c) + \varepsilon
f(c)\ – \varepsilon < f(x) < f(c) + \varepsilon![]() c – \delta < x < c + \delta
c – \delta < x < c + \delta![]() x \in S
x \in S![]() f(x)\ \in\ N(f(c),\ \varepsilon)
f(x)\ \in\ N(f(c),\ \varepsilon)![]() x \in N(c, \delta) \cap S
x \in N(c, \delta) \cap S![]() f
f![]() S
S![]() S
S![]() S \subset \mathbb{R}
S \subset \mathbb{R}![]() f : S \to \mathbb{R}
f : S \to \mathbb{R}![]() S
S![]() f
f![]() S
S![]() S
S![]() \mathbb{R}
\mathbb{R}![]() f(S)
f(S)![]() \mathbb{R}
\mathbb{R}![]() f\left(S\right)
f\left(S\right) \sigma = \{I : \alpha \in \Lambda\}
\sigma = \{I : \alpha \in \Lambda\}![]() f(S)\ \subset\ \bigcup_{\alpha\in\Lambda} I_\alpha
f(S)\ \subset\ \bigcup_{\alpha\in\Lambda} I_\alpha![]() \sigma
\sigma![]() f(S)
f(S)![]() a \in S
a \in S![]() f(a)\ \in\ f(S)
f(a)\ \in\ f(S)![]() I_{\alpha'}
I_{\alpha'}![]() \sigma
\sigma![]() f(S) \in I_{\alpha'}
f(S) \in I_{\alpha'}![]() I_{\alpha'}
I_{\alpha'}![]() f(a)
f(a)![]() \varepsilon_a
\varepsilon_a![]() \delta_a
\delta_a![]() f(x)\ \in\ N(f(a),\ \varepsilon_a)\ \subset\ I_\alpha'
f(x)\ \in\ N(f(a),\ \varepsilon_a)\ \subset\ I_\alpha'![]() x \in N(a,\delta_a) \cap S
x \in N(a,\delta_a) \cap S![]() C = \{N(a, \delta_a) : a \in S\}
C = \{N(a, \delta_a) : a \in S\}![]() S
S![]() S
S![]() C
C![]() C' = \{N(a, \delta_a) : i = 1, 2, \ldots, m\}
C' = \{N(a, \delta_a) : i = 1, 2, \ldots, m\}![]() a_i \in S
a_i \in S![]() \delta_{a_i} > 0
\delta_{a_i} > 0![]() i = 1, 2, \ldots, m
i = 1, 2, \ldots, m![]() C'
C'![]() S
S![]() S \subset \bigcup_{i=1}^{m}{N(a_i,\ \delta_{a_i})}
S \subset \bigcup_{i=1}^{m}{N(a_i,\ \delta_{a_i})}![]() f(S)
f(S)![]() f(x)
f(x)![]() x \in S
x \in S![]() x \in N(a_p,\ \delta_{a_p})
x \in N(a_p,\ \delta_{a_p})![]() p = 1, 2, \ldots, m
p = 1, 2, \ldots, m![]() x \in N(a_p, \varepsilon_{a_p}) \cap S
x \in N(a_p, \varepsilon_{a_p}) \cap S![]() p = 1, 2, \ldots, m
p = 1, 2, \ldots, m![]() f(x) \in\ N(f(a_p),\ \varepsilon_{a_p})\ \subset\ I_{{\alpha'}_p}
f(x) \in\ N(f(a_p),\ \varepsilon_{a_p})\ \subset\ I_{{\alpha'}_p}![]() p = 1, 2, \ldots, m
p = 1, 2, \ldots, m![]() f(x) \in\ f(S)\ \Rightarrow\ f(x) \in\ I_{{\alpha'}_p}
f(x) \in\ f(S)\ \Rightarrow\ f(x) \in\ I_{{\alpha'}_p}![]() p = 1, 2, \ldots, m
p = 1, 2, \ldots, m![]() f(S) \subset\ \bigcup_{P=1}^{m}{\ I_{{\alpha'}_p}}
f(S) \subset\ \bigcup_{P=1}^{m}{\ I_{{\alpha'}_p}}![]() \sigma' = \{{I}_{{\alpha'}_1},\ I_{{\alpha'}_2}, \ldots,\ I_{{\alpha'}_m}\}
\sigma' = \{{I}_{{\alpha'}_1},\ I_{{\alpha'}_2}, \ldots,\ I_{{\alpha'}_m}\}![]() \sigma
\sigma![]() f(S)
f(S)![]() \sigma'
\sigma'![]() \sigma
\sigma![]() f(S)
f(S)![]() f(S)
f(S)![]() \mathbb{R}
\mathbb{R}![]() \mathbb{R}
\mathbb{R}![]() \sup{f(S)}
\sup{f(S)}![]() f(S)
f(S)![]() f(S)
f(S) \mathbb{R}
\mathbb{R}![]() \mathbb{R}
\mathbb{R}![]() f : S \to \mathbb{R}
f : S \to \mathbb{R}![]() S (\subset R)
S (\subset R)![]() f(S)
f(S)![]() S
S![]() \mathbb{R}
\mathbb{R} (2, 3]
(2, 3] \mathbb{R}
\mathbb{R}![]() S = \left\lbrace x \in (0, 1): x \neq \frac{1}{n}, n \in \mathbb{N}\right\rbrace
S = \left\lbrace x \in (0, 1): x \neq \frac{1}{n}, n \in \mathbb{N}\right\rbrace![]() \sigma = \left\lbrace \left(\frac{1}{n+1},\ \frac{1}{n}\right) : n \in \mathbb{N}\right\rbrace
\sigma = \left\lbrace \left(\frac{1}{n+1},\ \frac{1}{n}\right) : n \in \mathbb{N}\right\rbrace![]() \sigma
\sigma![]() S
S![]() \sigma
\sigma![]() S
S![]() A = \left[\frac{1}{2},\ \frac{7}{2}\right]
A = \left[\frac{1}{2},\ \frac{7}{2}\right]![]() B =\left(1,\ \frac{9}{2}\right)
B =\left(1,\ \frac{9}{2}\right)![]() A \cup B
A \cup B![]() A
A![]() \mathbb{R}
\mathbb{R}![]() B
B![]() \mathbb{R}
\mathbb{R}![]() A \cup B
A \cup B![]() \mathbb{Q}
\mathbb{Q} A
A![]() B
B![]() \mathbb{R}
\mathbb{R}![]() A \cap B
A \cap B![]() \mathbb{R}
\mathbb{R}![]() \mathbb{R}$?
\mathbb{R}$?
Bibliography
- An introduction to functional analysis, By Charles Swartz.
- Introduction to Topology, By Bert Mendelson.
- The Elements of Real Analysis, R.G
- Real Analysis, H.L. Royden
Thank you for reading this article. We will meet next time with a new article
Also, you may want to check our blog posts about Fourier Series, Riemann Integral, Lebesgue Outer Measure, and All The Logarithm Rules You Know and Don't Know About
And don't forget to join us on our Facebook page stay updated on any new articles and a lot more!!!!!
millerhumbecioned.blogspot.com
Source: https://www.mathacademytutoring.com/blog/compact-sets-and-continuous-functions-on-compact-sets
0 Response to "Show That the Lower Level Sets of a Continuous Function Are Closed"
Post a Comment